Formulario de Regresion Lineal
Especial | A | B | C | D | E | F | G | H | I | J | K | L | M | N | Ñ | O | P | Q | R | S | T | U | V | W | X | Y | Z | TODAS
C |
|---|
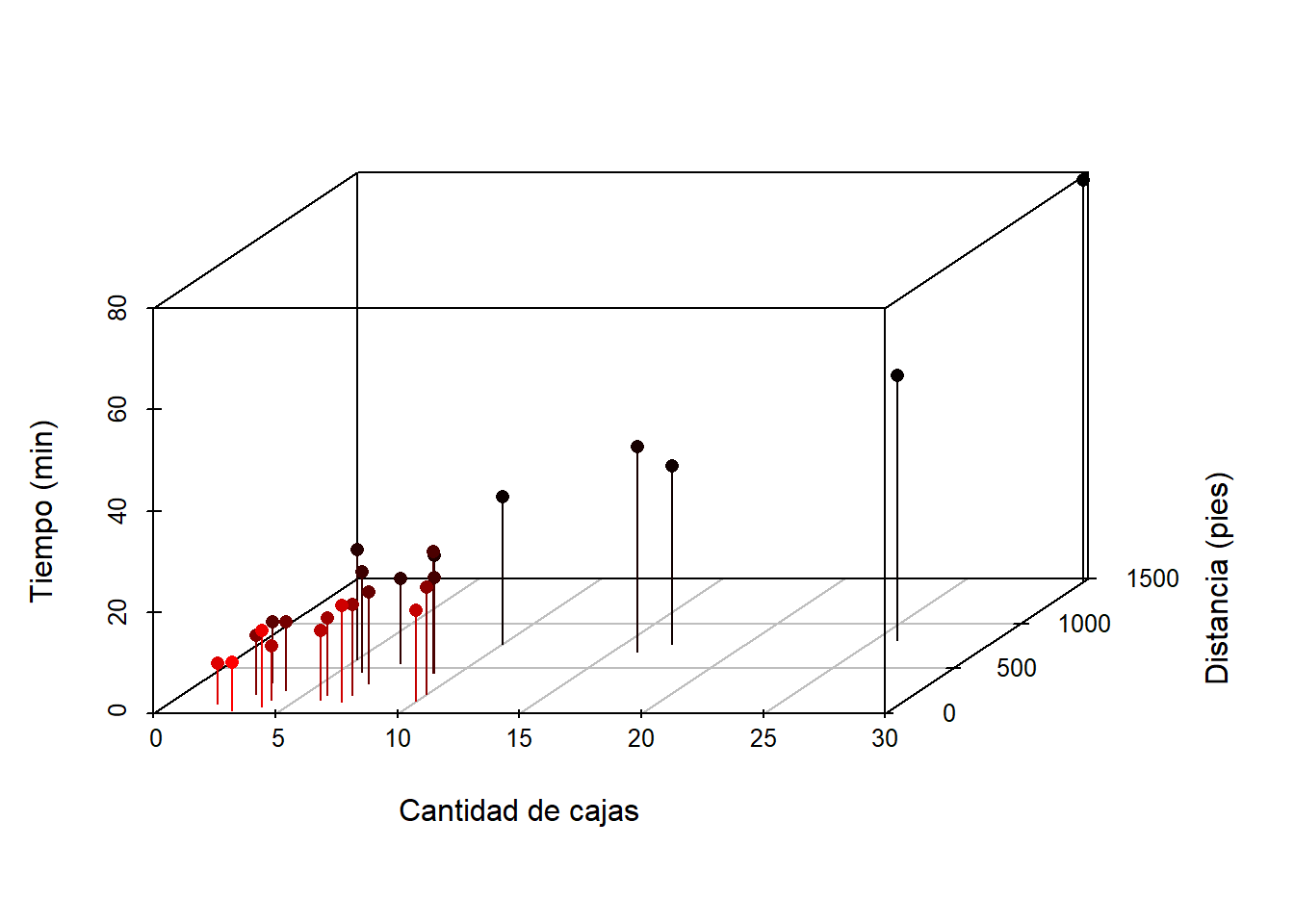
Coeficiente de determinaciónEn estadística, el coeficiente de determinación, denominado R² y pronunciado R cuadrado, es un estadístico usado en el contexto de un modelo estadístico cuyo principal propósito es predecir futuros resultados o probar una hipótesis. El coeficiente determina la calidad del modelo para replicar los resultados, y la proporción de variación de los resultados que puede explicarse por el modelo.1 Hay varias definiciones diferentes para R² que son algunas veces equivalentes. Las más comunes se refieren a la regresión lineal. En este caso, el R² es simplemente el cuadrado del coeficiente de correlación de Pearson, lo cual es sólo cierto para la regresión lineal simple. Si existen varios resultados para una única variable, es decir, para una X existe una Y, Z... el coeficiente de determinación resulta del cuadrado del coeficiente de determinación múltiple. En ambos casos el R² adquiere valores entre 0 y 1. Existen casos dentro de la definición computacional de R² donde este valor puede tomar valores negativos.2 Caso generalUn modelo estadístico se construye para explicar una variable aleatoria, que llamaremos dependiente, a través de otras variables aleatorias a las que llamaremos factores. Dado que podemos predecir una variable aleatoria mediante su media y que, en este caso, el error cuadrático medio es su varianza, el máximo error cuadrático medio que podemos aceptar en un modelo para una variable aleatoria que posea los dos primeros momentos es la varianza. Para estimar el modelo haremos varias observaciones de la variable a predecir y de los factores. A la diferencia entre el valor observado de la variable y el valor predicho la llamaremos residuo. La media cuadrática de los residuos es la varianza residual. Si representamos por la varianza de la variable dependiente Se mide en tantos por ciento. Si la varianza residual es cero, el modelo explica el 100% de valor de la variable; si coincide con la varianza de la variable dependiente, el modelo no explica nada y el coeficiente de determinación es del 0%. En variables económicas y financieras, suele ser difícil conseguir un coeficiente de determinación mayor de un 30%. Para la regresión linealPara la regresión basta con hacer el cuadrado del coeficiente de correlación de Pearson. Donde: Modelo linealEn un modelo lineal, la variable dependiente y yi=∑i=1mβjxij+εi{\displaystyle y_{i}=\sum _{i=1}^{m}\beta _{j}x_{ij}+\varepsilon _{i}} Estos errores se llaman residuos. La varianza residual es la varianza de estos residuos. σr2=∑i=1nεi2=ε′ε=(y−Xβ)′(y−Xβ){\displaystyle \sigma _{r}^{2}=\sum _{i=1}^{n}\varepsilon _{i}^{2}=\mathbf {\varepsilon } '\mathbf {\varepsilon } =(\mathbf {y} -\mathbf {X} \mathbf {\beta } )'(\mathbf {y} -\mathbf {X} \mathbf {\beta } )} ∑j=1nβjxij{\displaystyle \sum _{j=1}^{n}\beta _{j}x_{ij}} εi{\displaystyle \varepsilon _{i}} Sumando estas dos partes, obtenemos yi{\displaystyle y_{i}} El valor del coeficiente de determinación aumenta cuando se incluyen nuevas variables en el modelo, incluso cuando éstas son poco significativas o tienen poca correlación con la variable dependiente. El coeficiente de determinación corregido mide el porcentaje de variación de la variable dependiente (al igual que el coeficiente de determinación) pero tiene en cuenta además el número de variables incluidas en el modelo. | |
F |
|---|
Factor de inflación de la varianza (VIF)n estadística, el factor de inflación de la varianza (FIV, a veces también conocido por su nombre en inglés, variance inflation factor, y de ahí VIF) cuantifica la intensidad de la multicolinealidad en un análisis de regresión normal de mínimos cuadrados. Proporciona un índice que mide hasta qué punto la varianza (el cuadrado de la desviación estándar estimada) de un coeficiente de regresión estimado se incrementa a causa de la colinealidad. Considerando el siguiente modelo lineal con k variables independientes
El error estándar de la estimación de βj es la raíz cuadrada de los j+1, j+1 como elemento de s2(X′X)−1, donde s es la raíz del error cuadrático medio (RECM), teniendo en cuenta que RECM2 es un estimador insesgado de la varianza del error σ2{\displaystyle \sigma ^{2}} donde Rj2 es el múltiplo R2 para la regresión de Xj sobre otras covariables (una regresión que no involucra la respuesta de la variable Y). Esta identidad separa las influencias de varios factores diferentes en la varianza de la estimación del coeficiente:
Se pueden calcular los k factores de inflación de la varianza diferentes (uno para cada Xi) en tres pasos: Primer pasoEn primer lugar se realiza una regresión de mínimos cuadrados que tenga a Xi como una función de las demás variables explicativas de la primera ecuación. Si i = 1, por ejemplo, la ecuación sería:
donde c0 es una constante y e es el error. Segundo pasoEn segundo lugar, se calcula el factor de inflación de la varianza para β^i{\displaystyle {\hat {\beta }}_{i}}
donde R2i es el coeficiente de determinación de la ecuación de regresión del primer paso, con Xi{\displaystyle X_{i}} Tercer pasoSe analiza la magnitud de la multicolinealidad considerando el tamaño de FIV(β^i){\displaystyle \operatorname {FIV} ({\hat {\beta }}_{i})} | |
V |
|---|
Variables dependientes e independientesEn un experimento, una variable, manipulada por un experimentador, se llama variable independiente. La variable dependiente es el evento que se espera que cambie cuando se manipula la variable independiente.5 En las herramientas de minería de datos (para estadística multivariante y aprendizaje automático), a la variable dependiente se le asigna un rol como variable objetivo (o en algunas herramientas como característica objetivo), mientras que a una variable independiente se le puede asignar un rol como variable regular.6 Se proporcionan valores conocidos para la variable objetivo para el conjunto de datos de formación y el conjunto de datos de prueba, pero deben predecirse para otros datos. La variable objetivo se utiliza en los algoritmos de aprendizaje supervisado, pero no en el aprendizaje no supervisado. | |
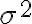
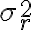
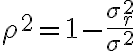
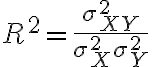
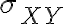
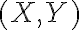
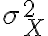
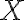
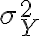
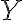
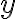
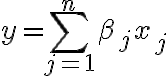









![{\displaystyle {\bar {R}}^{2}=1-{N-1 \over N-k-1}[1-R^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/538bea5becea70b5ed16c4f52814b0c2fb2ab8b7)








